Answer:
81.64%
Explanation:
Data provided in the question:
Standard deviation, s = 24 rooms
Sample size, n = 16 days
Mean = 48 rooms
calculated an interval = 40 to 56
Now,
Level of confidence = 100(1 - α)%
Confidence interval = Mean ±
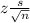
Thus,
Mean -
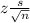 = 40
= 40
and,
Mean +
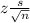 = 56
= 56
or
48 +
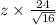 = 56
= 56
or
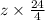 = 8
= 8
or
z = 1.33
for z = 1.33 , we have
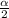 = 0.918 [from standard z table]
= 0.918 [from standard z table]
or
α = 0.1836
Therefore,
Level of confidence = 100(1 - 0.1836)%
or
Level of confidence = 81.64%