Answer:
Starting point is (0, 210).
Rate of change is 0.12 or 12%.
Explanation:
Given:
The given function is:
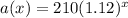
The above function represents an exponential growth function of the form:

Now, we need to convert the given function in the standard form.
So, we write 1.12 as sum of 1 and a number.
So, 1.12 = 1 + 0.12
Therefore, the given function can be rewritten as:

Now, on comparing it with the general form, we conclude:
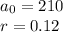
Therefore, the rate of change is 0.12 or 12 %.
Also, the starting point on the graph will be when 'x' is 0. So, the starting point is (0,210).