Answer:
The area = 182.52 sq units.
Explanation:
- Area of regular polygon can be found by splitting into smaller triangles.
- Each triangle has base as side of polygon and vertex as center of polygon.
now consider ΔOAB,
we know ∠AOB =
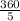 ° =72°
° =72°
(this is due to symmetry)
as ∠AOD = (∠AOB)/2 = 36°
Now we know AD=AB/2 =
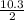 =5.15 m
=5.15 m
using trignometric relation tan(∠AOD) =

⇒OD =
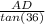 =
=
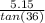
AREA OF TRIANGLE = BASE × HEIGHT /2
area of ΔOAD =
 × 5.15 ×
× 5.15 ×
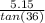
=

As there are 10 such triangles like ΔOAD
Total area =10×

= 182.525447428574