The farmer and daughter working together would take 6 days to plant the field
Solution:
Time taken by farmer to plant a field is 10 days
Time taken by his daughter to plant a field is 15 days
Now lets find L.C.M of 10 and 15
List all prime factors for each number.
Prime factorization of 10 = 2 x 5
Prime factorization of 15 = 3 x 5
For each prime factor, find where it occurs most often as a factor and write it that many times in a new list.
The new superset list is
2, 3, 5
Multiply these factors together to find the LCM.
LCM = 2 x 3 x 5 = 30
Thus L.C.M of 10 and 15 is 30
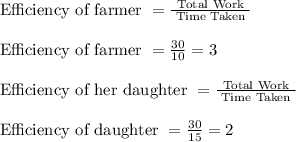
When both of them work together:
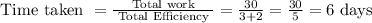
Hence, both of them can complete the work in 6 days