Question

Help with functions?

Answer 1

The function g(x) = - x² + 14x + 39 is at a minimum when x = 7 is not true i.e. false.

Explanation:

The function is given to be g(x) = - x² + 14x + 39 .......... (1)

Now, the condition for maxima or minima is
`g'(x) = (dg(x))/(dx) = 0`.

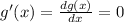Now, differentiating equation (1) we get, g'(x) = - 2x + 14 ........ (2)

Hence, for maxima or minima g'(x) = 0 = - 2x + 14

⇒ x = 7

Now, from equation (2) and differentiating both sides with respect to x again
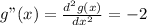`g` < 0

Therefore,the function g(x) has maxima at x = 7

Therefore, the function g(x) = - x² + 14x + 39 is at a minimum when x = 7 is not true i.e. false.