Question

Given the values in the probability distribution table, determine the standard deviation.

A. 3.2
B. 13.9
C. 3.9
D. 2.0

Answer 1

1.96

Explanation:

Solution:-

- We will use the table given to determine the standard deviation of random variable x. From descriptive statistics we have the following formula for standard deviation (s.d) :

s.d (x) = sqrt ( Var(x) )

- The formula for Variance ( Var (x) ) is also taken from descriptive statistics as follows:

`Var(X) = E ( X^2) + [ E(X) ] ^2`

- Where,

`E ( X^2) = 0^2*0.15 + 1^2*0.07 + 2^2*0.19 + 3^2*0.09 + 4^2*0.16 + 5^2*0.23 +6^2*0.11 \\\\E ( X^2) = 13.91 \\\\`

`E(X) = 0*0.15\:+\:1*0.07\:+\:2*0.19\:+\:3\cdot \:0.09\:+\:4\cdot \:0.16\:+\:5\cdot \:0.23\:+6\cdot \:0.11\\\\E(X) = 3.17\\\\(E(X))^2 = 10.0489`

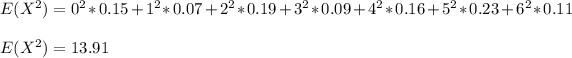
- So the variance is:

Var ( X ) = 13.91 - 10.0489 = 3.8611

s.d (x) = √3.8611 = 1.96

Answer 2

D. 2.0 is the right answer

Explanation:

Note: All decimals were converted to fractions.

The standard deviation of the given distribution is:

σ=1.965