Question

Two gardeners can do the weekly yard maintenance in 8 minutes if they work together. The older gardener takes 12 minutes more than the younger gardener to finish the job by himself. How long does it take for each gardener to do the weekly yard maintainence individually?

Answer 1

Let x be the time taken( in minutes ) by younger gardener,

So, the one minute work of younger gardener =
`(1)/(x)`

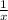
Also, the time taken by older gardener = (x+12) minutes ( given ),

So, the one minute work of older gardener =
`(1)/(x+12)`

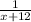
Total work done in one minute =
`(1)/(x)+(1)/(x+12)`

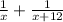
Now, total time taken = 8 minutes,

Total work done in one minute =
`(1)/(8)`

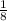
Thus,

`(1)/(x)+(1)/(x+12)=(1)/(8)`

`(x+12+x)/(x^2+12x)=(1)/(8)`

`(2x+12)/(x^2+12x)=(1)/(8)`

`16x + 96 = x^2+12x`

`x^2 -4x -96=0`

`x^2 - 12x + 8x - 96=0`

`x(x-12) + 8(x-12)=0`

`(x+8)(x-12)=0`

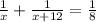
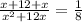
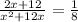
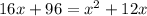
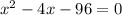
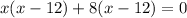
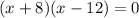
By zero product product property,

x + 8 =0 or x - 12 =0

⇒ x = -8 ( not possible ), x = 12

Hence, the time taken by younger gardener = 12 minutes,

And, the time taken by older gardener = 12 + 12 = 24 minutes.