Question

A satellite and the International Space Station have the same mass and are going around Earth in concentric orbits. The distance of the satellite from Earth\'s center is twice that of the International Space Station\'s distance. What is the ratio of the centripetal force acting on the satellite compared to that acting on the International Space Station?

A) 0.25

B) 1

C) 2

D) 0.5

E) 4

Answer 1

A. 0.25

Step-by-step explanation:

G = Gravitational constant

M = Mass of Earth

m = Mass of space station = Mass of satellite

r = Distance between Earth and object

Centripetal force on Space Station

`F_(ss)=(GMm)/(r^2)`

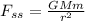
Centripetal force on satellite

`F_(s)=(GMm)/((2r)^2)\\\Rightarrow F_(ss)=(GMm)/(4r^2)`

Divinding the forces we get

`(F_s)/(F_(ss))=((GMm)/(4r^2))/((GMm)/(r^2))\\\Rightarrow (F_s)/(F_(ss))=(1)/(4)=0.25`

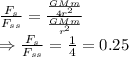
The ratio of centripetal force acting on the satellite compared to that acting on the International Space Station is 0.25