Question

In 1994 the performer Rod Stewart drew over 3 million people to a concert in Rio de Janeiro, Brazil.

(a) If the people in the group had an average mass of 80.0 kg, what collective gravitational force would the group have on a 4.50-kg eagle soaring 3.00 Ã 10 2 m above the throng? If you treat the group as a point object, you will get an upper limit for the gravitational force.

(b) What is the ratio of that force of attraction to the force between Earth and the eagle

Answer 1

Answers:

a)
`8.009(10)^(-7) N`

b)
`1.8(10)^(-8)`

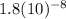
Step-by-step explanation:

a) Accoding to the Universal Law of Gravitation we have:

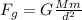`F_(g)=G(Mm)/(d^2)` (1)

Where:

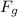`F_(g)` is the gravitational force between the eagle and the throng

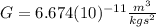`G=6.674(10)^(-11)(m^(3))/(kgs^(2))` is the Universal Gravitational constant

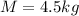`M=4.5 kg` is the mass of the eagle

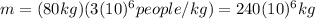`m=(80 kg)(3(10)^(6) people/kg)=240(10)^(6) kg` is the mass of the throng

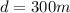`d=300 m` is the distance between the throng and the eagle

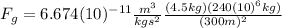`F_(g)=6.674(10)^(-11)(m^(3))/(kgs^(2)) ((4.5 kg)(240(10)^(6) kg))/((300 m)^(2))` (2)

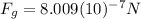`F_(g)=8.009 (10)^(-7) N` (3) As we can see the gravitational force between the eagle and the throng is quite small.

b) The attraction force between the eagle and Earth is the weight
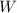`W` of the eagle, which is given by:

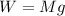`W=Mg` (4)

Where
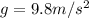`g=9.8 m/s^(2)` is the acceleration due gravity on Earth

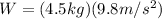`W=(4.5 kg)(9.8 m/s^(2))` (5)

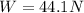`W=44.1 N` (6)

Now we can find the ratio between
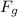`F_(g)` and
`W`:

`(F_(g))/(W)=(8.009 (10)^(-7) N)/(44.1N)`

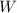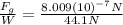
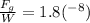`(F_(g))/(W)=1.8(^(-8))` As we can see this ratio is also quite small