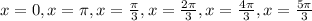Question

Find all solutions to the equation in the interval [0, 2π). (3 points) cos 4x - cos 2x = 0 0, two pi divided by three. , four pi divided by three. pi divided by six , pi divided by two , five pi divided by six , seven pi divided by six , three pi divided by two , eleven pi divided by six 0, pi divided by three. , two pi divided by three. , π, four pi divided by three. , five pi divided by three. No solution

Answer 1

`x=0,x=\pi,x=(\pi)/(3),x=(2\pi)/(3),x=(4\pi)/(3),x=(5\pi)/(3)`

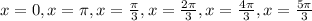
Explanation:

This is a trigonometric equation where we need to use the cosine of the double-angle formula

`cos4x=2cos^22x-1`

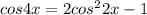
Replacing in the equation

`cos4x - cos2x = 0`

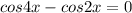
We have

`2cos^22x-1 - cos 2x = 0`

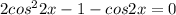
Rearranging

`2cos^22x - cos 2x-1 = 0`

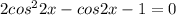
A second-degree equation in cos2x. The solutions are:

`cos2x=1,cos2x=-(1)/(2)`

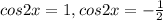
For the first solution

cos2x=1 we find two solutions (so x belongs to [0,2\pi))

`2x=0, 2x=2\pi`

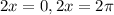
Which give us

`x=0,x=\pi`

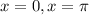
For the second solution

`cos2x=-(1)/(2)`

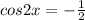
We find four more solutions

`2x=(2\pi)/(3),2x=(4\pi)/(3),2x=(8\pi)/(3),2x=(10\pi)/(3)`

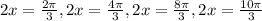
Which give us

`x=(\pi)/(3),x=(2\pi)/(3),x=(4\pi)/(3),x=(5\pi)/(3)`

All the solutions lie in the interval
`[0,2\pi)`

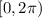
Summarizing. The six solutions are

`x=0,x=\pi,x=(\pi)/(3),x=(2\pi)/(3),x=(4\pi)/(3),x=(5\pi)/(3)`