Question

What is (2,7) rotated 90% clockwise

Answer 1

The required point is, (7, -2)

Explanation:

The straight line passing through (0,0) and (2,7) is,

y =
`(\frac {7 -0}{2-0}) * x`

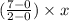
⇒ y = 3.5x --------------(1)

Now, the straight line perpendicular to this line and passing through (0, 0) is

y =
`(\frac {-1}{3.5}) * x`

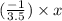
⇒ 7y + 2x = 0 -------------(2)

Let, (h,k) be the required point.

then, it is on the line 7y + 2x = 0

⇒7k + 2h = 0

⇒k =
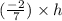`(\frac {-2}{7}) * h` ------------(3)

Again, distance from (0,0) of (h, k) is same as that of (2,7)

⇒
`h^(2) + k^(2) = 4 + 49 = 53`

⇒
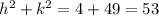
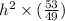`h^(2) * (\frac {53}{49})` = 53 [putting the value of k from (3)]

⇒
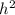`h^(2)` = 49

⇒h = 7 [since, (h,k) is in 4th quadrant, so,h >0]

So, k = -2 [putting the value of h in (3)]

So, the required point is, (7, -2)