Question

Prove that 2√3÷5 is irrational​

Answer 1

To prove:

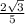`(2√(3))/(5)` is irrational number.

Proof:

Let us first assume
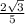`(2√(3))/(5)` is a rational number.

So, it can be written as:

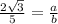`(2√(3))/(5)=(a)/(b)` where
`b\\eq0`

Multiplying both sides by 5.

`5* (2√(3))/(5)=5* (a)/(b)`

`2√(3)=(5a)/(b)`

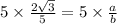
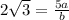
Dividing both sides by 2.

`(2√(3))/(2)=(5a)/(2b)`

`√(3)=(5a)/(2b)`

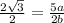
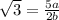
We see that
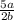`(5a)/(2b)` is a rational number as it is in the
`(p)/(q)` form but we know
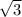`\sqrt3` is irrational which makes the equation false making it contradicting with our assumption.

Thus our assumption is wrong.

Hence
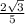`(2√(3))/(5)` is an irrational number.