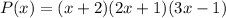Question

If P(x)=6x^3=13x^2+x-2, and P(-2)=0, then the factorization of P(x) is

Answer 1

Factorization of
`P(x)=(x+2)(2x+1)(3x-1)`

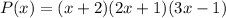
Explanation:

Given:

The given polynomial is
`P(x)=6x^3+13x^2+x-2`

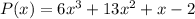
Also,
`P(-2)=0`

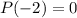
Since, for
`x=-2`,
`P(x)` is 0, therefore,
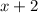`x+2` is a factor of the polynomial.

Now, let us divide the given polynomial by
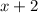`x+2` using long division method. Therefore,

`(6x^3+13x^2+x-2)/(x+2)=6x^2+x-1`

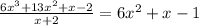
The process of long division is shown below.

Now, factoring the quotient
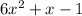`6x^2+x-1`, we get

`6x^2+x-1=6x^2+3x-2x-1=3x(2x+1)-1(2x+1)=(3x-1)(2x+1)`

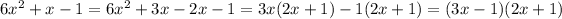
Therefore, the factors of polynomial
`P(x)` are
`(x+2),(2x+1),\ and\ (3x-1)`

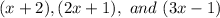
Hence, the factorization of
`P(x)` is:

`P(x)=(x+2)(2x+1)(3x-1)`