Question

Which of the following point-slope form equations could be produced with the points (2, -6) and (4, -3)?

y - 6 = 3/2(x + 2)
y - 6 = 3/2(x - 2)
y + 6 = 3/2(x - 2)
y + 6 = -3/2(x + 2)

Answer 1

C) y+6=3/2(x-2)

Explanation:

y-y1=m(x-x1)

m=slope & (x1, y1) is a point on the line

m=(y2-y1)/(x2-x1)

m=(-3-(-6))/(4-2)

m=(-3+6)/2

m=3/2

y-(-6)=3/2(x-2)

y+6=3/2(x-2)

Answer 2

Option 3

The point slope form of the given points (2, -6) and (4, -3) is
`y+6=(3)/(2)(x-2)`

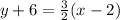
Solution:

Given that two points are (2, -6) and (4, -3)

We have to find the point slope form

The point-slope of the line is given as:

`y - y_1 = m(x - x_1)`

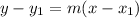
Where m is the slope of the given line.

So now to write the given points in point intercept form we need to find the slope, m

The slope of line is given as:

`m=(y_(2)-y_(1))/(x_(2)-x_(1))`

`\text { Here } x_(1)=2 ; y_(1)=-6 ; x_(2)=4 ; y_(2)=-3`

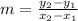
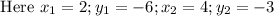
Plugging in the values, we get

`m=(-3-(-6))/(4-2)=(3)/(2)`

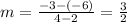
So, the slope of the given line is
`(3)/(2)`

Now, we need to find the point slope form. For that purpose we can use either of the points, but since in the answer options they have used the 1st point we will do so too.

Therefore, the point slope form is:

`\begin{array}{l}{y-(-6)=(3)/(2)(x-2)} \\\\ {y+6=(3)/(2)(x-2)}\end{array}`

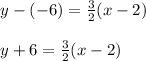
From the given options we can see that the correct answer is option 3.