Question

Triangular numbers can be represented with equilateral triangles formed by dots. The first five triangular numbers are 1, 3, 6, 10, and 15.?Is there a direct variation between a triangular number and its position in the sequence? Explain your reasoning.

Answer 1

Yes, those are the first triangular numbers.

There is a relation between the number and its position but isn't direct.

Explanation:

The triangular numbers can be represented by equilateral triangles, but also can be represented by:

`T_(n) = (n(n+1))/(2)`

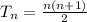
where:

n, represents the position

T represent the triangular number.

As you may see, the equation of triangular numbers is not a straight line. It is a parable. For that reason there isn't a direct variation.

Answer 2

No, the triangular numbers are not a direct variation. There is not a constant of variation between a number and its position in the sequence. The ratios of the numbers to their positions are not equal. Also, the points (1, 1), (2, 3), (3, 6), and so on, do not lie on a line.

Explanation: