Question

A license plate consists of 2 letters followed by 4 numbers, and to avoid confusion, the numbers 1 and 0 are not used. How many different license plates are possible? How many plates are possible if repetition is not allowed?

Answer 1

There are 2768896 combinations with repetitions and 1092000 with no repetitions.

Solution:

Given, A license plate consists of 2 letters followed by 4 numbers,

And to avoid confusion, the numbers 1 and 0 are not used.

We have to find how many different license plates are possible? How many plates are possible if repetition is not allowed?

Now let us find in repetition case.

Total we have 6 places out of which 1st two are alphabets and remaining are numbers from 2 to 9.

For 1st place there are 26 possibilities. (A to Z)

For 2nd place there are again 26 possibilities as repetition is allowed.

For 3rd place there are 8 possibilities (2 to 9)

For 4th 5th and 6th places also 8 possibilities as repetition allowed.

Then, total possible combinations are:

`26 * 26 * 8 * 8 * 8 * 8 = 2768896 combinations`

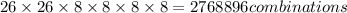
Now let us find in no repetition case.

Total we have 6 places out of which 1st two are alphabets and remaining are numbers from 2 to 9.

For 1st place there are 26 possibilities. (A to Z)

For 2nd place there are only 25 possibilities as repetition is not allowed. And one of 26 is already taken.

For 3rd place there are 8 possibilities (2 to 9)

For 4th place there are only 7 chances as one or 8 is already taken and repetition is not allowed.

For 5th place there are 6 chances because of the same reason.

For 6th place there are 5 chances finally.

Then, total possibilities =
`26 * 25 * 8 * 7 * 6 * 5 = 1092000 \text{combinations}`

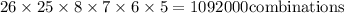
Hence, there are 2768896 combinations with repetitions and 1092000 with no repetitions.