Question

How much ice (at 0°C) must be added to 1.75 kg of water at 77 °C so as to end up with all liquid at 26 °C? (ci = 2000 J/(kg.°C), cw = 4186 J/(kg.°C), Lf= 3.35 × 10 5 3.35×105 J/kg, Lv= 2.26 × 10 6 2.26×106 J/kg)

Answer 1

To solve this problem it is necessary to apply the conservation equations of Energy.

By definition we know that the energy that is lost by water is totally equivalent to the energy gained by ice.

The energy lost by water could be defined as

`E_w = m_wC_w\Delta T`

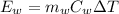
Where,

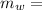`m_w=`mass of water

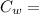`C_w =` Specific Heat of Water

`\Delta T =` Change in Temperature

On the other hand the energy gained by ice can be defined as

`E_i = m_i L_f +m_i C_i \Delta T`

Where,

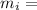`m_i =` Mass of ice

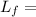`L_f =` Latent heat of fusion

`C_i =`Specific heat of Ice

`\Delta T =` Change in Temperature

As the two energies are in balance then

`E_w = E_i`

`m_wC_w\Delta T=m_i L_f +m_i C_i \Delta T`

`m_wC_w\Delta T=m_i (L_f +C_i \Delta T)`

`(1.75)(4186)(77-26)= m_i (3.35*10^5+2000*(26-0))`

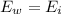
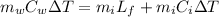
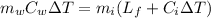
Re-arrange to find
`m_i,`

`m_i = ((1.75)(4186)(77-26))/((3.35*10^5+2000*(26-0)))`

`m_i = 0.9653Kg`

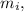
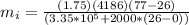
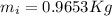
Therefore there must be 0.9653Kg of Ice