Question

11. Refer to the rectangle at the right. Suppose the side lengths

are doubled.

a. Find the percent of change in the perimeter.

b. Find the percent of change in the area.


What’s the answer?

Answer 1

Answer: a) The percent of change in perimeter is 100%.

b) The percent of change in area is 300%.

Explanation:

Since we have given that

if the side lengths of rectangle get doubled.

Let the length be 'x'.

Let the breadth be 'y'.

So, Perimeter of rectangle would be

`2(x+y)`

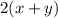
Area of rectangle would be

`xy`

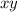
After doubling the lengths,

Length becomes '2x'.

Width becomes '2y'.

So, perimeter becomes

`2(2x+2y)\\\\=4(x+y)`

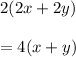
Area becomes

`2x* 2y\\\\=4xy`

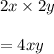
a. Find the percent of change in the perimeter.

`(4(x+y)-2(x+y))/(2(x+y))* 100\\\\=(2(x+y))/(2(x+y))* 100\\\\=100\%`

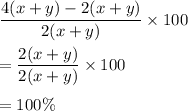
Hence, the percent of change in perimeter is 100%.

b. Find the percent of change in the area.

`(4xy-xy)/(xy)* 100\\\\=(3xy)/(xy)* 100\\\\=300\%`

Hence, the percent of change in area is 300%.