Question

Calculate the breadth B ( in degrees of 2θ ), due to the small crystal effect alone, of the powder pattern lines of particles of diameter 1000, 750, and 250Å. Assume θ=45° and λ=1.5 Å. For particles 250 Å in diameter, calculate the breadth B for θ=10, 45, and 80°.

Answer 1

For differents τ:

τ = 1000 Å → B = 0.11°

τ = 750 Å → B = 0.15°

τ = 250 Å → B = 0.44°

For differents Θ:

Θ = 10° → B = 0.31°

Θ = 45° → B = 0.44°

Θ = 80° → B = 1.78°

Explanation:

To factor B is related to the size of particles, Θ, and λ by the Scherrer equation:

`\tau = (K \lambda)/( B cos(\theta))`

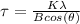
where τ: size of the particles, λ: is the wavelenght of the X-Rays, B: is the line broadening at half the maximum intensity, Θ: angle of incidence and K: is a shape factor with typical value of 0.9

`B = (K \lambda)/( \tau cos(\theta))`

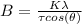
Now, factor B for the diameter of the particles (τ) is:

τ = 1000 Å:

`B = (0.9 \cdot 1.5)/(1000 \cdot cos(45)) = 1.91\cdot 10^(-3) rad = 0.109 ^(\circ)`

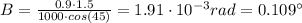
τ = 750 Å:

`B = (0.9 \cdot 1.5)/(750 \cdot cos(45)) = 2.54\cdot 10^(-3) rad = 0.146 ^(\circ)`

τ = 250 Å:

`B = (0.9 \cdot 1.5)/(250 \cdot cos(45)) = 7.64\cdot 10^(-3) rad = 0.438 ^(\circ)`

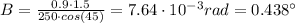
For τ = 250 Å, factor B for angles of incidence is:

Θ = 10°:

`B = (0.9 \cdot 1.5)/(250 \cdot cos(10)) = 5.48 \cdot 10^(-3) rad = 0.314 ^(\circ)`

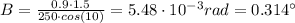
Θ = 45°:

B = 0.438°

Θ = 80°:

`B = (0.9 \cdot 1.5)/(250 \cdot cos(80)) = 0.031 rad = 1.78 ^(\circ)`

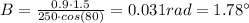
Have a nice day!