Question

A wheel is turning about an axis through its center with constant angular acceleration. Starting from rest, at t = 0, the wheel turns through 8.20 revolutions in 12.0 s. At t = 12.0 s the kinetic energy of the wheel is 36.0 J. For an axis through its center, what is the moment of inertia of the wheel?

Answer 1

I=0.489 kg.m²

Step-by-step explanation:

Given that

Initial speed of wheel (ω₁)= 0 rad/s

θ = 8.2 rev in t= 12 s

We know that

1 rev = 2π rad

8.2 rev = 16.4 π rad

θ =16.4 π rad

Lets take angular acceleration of wheel is α rad/s²

We know that if angular acceleration is constant

`\theta=\omega_1t+(1)/(2)\alpha t^2`

Now by putting the values

`\theta=\omega_1t+(1)/(2)\alpha t^2`

`16.4* \pi=0* 12+(1)/(2)\alpha * 12^2`

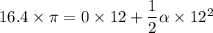
α =0.715 rad/s²

The final speed of the wheel at 12 s

ω₂=ω₁ + α t

ω₂ = 0 + 0.715 x 12

ω₂ =8.58 rad/s

The final kinetic energy of the wheel

`KE=(1)/(2)I\omega ^2`

`36=(1)/(2)I* 8.58^2`

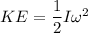
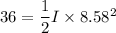
I=0.489 kg.m²

This is moment of inertia of the wheel .