Question

Use the Remainder Theorem to find the remainder for (2x^3-3x^2+6)/(x-1) and state whether or not the binomial is a factor of the polynomial.

Answer 1

Remainder= 0 and it is a polynomial

Explanation:

Got a 100% on edge 2020

Answer 2

Remainder= 5, and the binomial
`(x-1)` is not a factor of the given polynomial.

Explanation:

Given polynomial is
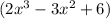`(2x^3-3x^2+6)` , we have to divide this with a binomial [tex}(x-1)[/tex] using remainder theorem.

Remainder theorem says if
`(x-a)` is a factor then remiander would be
`f(a)`

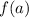
Therefore for
`(x-1), \ {we find}\  f(1)}`

`f(1)=(2* 1^3-3*1^2+6)\\1^3 =1\\1^2=1\\Substituting \ this \ above\\f(1)= (2-3+6)=5`

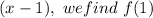
Thus the remainder is 5 and since it is not 0 , so the binomial
`(x-1)` is not a factor of the given polynomial.