Question

Find out the answers to this

Answer 1

`\tan \theta = - (1)/(5) = - 0.2`

`\cos \theta = 0.98`

`\sin \theta = - 0.196`

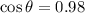
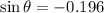
Explanation:

It is given that
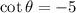`\cot \theta = - 5` and
`\theta` is in the fourth quadrant.

So, only
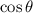`\cos \theta` will have positive value and
`\sin \theta`,
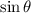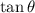`\tan \theta` will have negative value.

Now,
`\cot \theta = - 5`

⇒
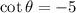
`\tan \theta = (1)/(\cot \theta) = -(1)/(5)` (Answer)

We know, that
`\sec^(2) \theta - \tan^(2) \theta = 1`

⇒
`\sec \theta = \sqrt{1 + \tan^(2) \theta } = \sqrt{1 + (- (1)/(5) )^(2) } = 1.019`

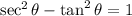
{Since,
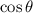`\cos \theta` is positive then
`\sec \theta` will also be positive}

⇒
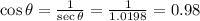`\cos \theta = (1)/(\sec \theta) = (1)/(1.0198) = 0.98` (Answer)

We know, that
`\csc^(2) \theta - \cot^(2) \theta = 1`

⇒
`\csc \theta = - \sqrt{1 + \cot^(2) \theta } = - \sqrt{1 + (- 5 )^(2) } = - 5.099`

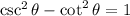
{Since,
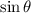`\sin \theta` is negative then
`\csc \theta` will also be negative}

⇒
`\sin \theta = (1)/(\csc \theta) = (1)/(- 5.099) = - 0.196` (Answer)