Question

4) We want a 99% confidence interval for the average amount of time (in minutes) spent commuting to work in a large city. The interval is to have a margin of error of no more than 3 minutes, and the amount of time spent commuting has a normal distribution with a standard deviation  = 18 minutes. What numbers of observations are required?

Answer 1

Answer: 239

Explanation:

Given : Confidence level : 99%

Significance level :
`\alpha=1-0.99=0.01`

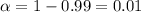
Margin of error : E = 3 minutes

Population standard deviation :
`\sigma=18`

To find : Numbers of observations are required. (Minimum Sample size)

Formula :
`n=((z_(\alpha/2)\cdot\sigma)/(E))^2`

Using z-value table,

Two-tailed z-value for
`\alpah=0.01` :
`z_(\alpha/2)=2.576`

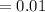Using given values , we get

`n=((2.576\cdot18)/(3))^2\\\\=(15.456)^2\\\\=238.887936\spprox239`

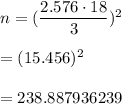
Hence, the minimum number of observation is required = 239