Question

Given the following information about a hypothesis test of the difference between two means based on independent random samples, what is the standard deviation of the difference between the two means? Assume that the samples are obtained from normally distributed populations having equal variances.H0: μA = μB, and H1: μA > μB X ¯ 1 = 12, X ¯ 2 = 9, s1= 5, s2 = 3, n1 =13, n2 =10.A. 1.792B. 1.679C. 2.823D. 3.210E. 1.478

Answer 1

Answer: B. 1.679

Explanation:

The standard deviation of the difference between the two means is given by :-

`SD (\overline{x}_1-\overline{x}_2)=\sqrt{(\sigma_1^2)/(n_1)+(\sigma_2^2)/(n_2)}`

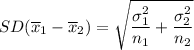
If true population standard deviations are not available , then

we estimate the standard error as

`SE (\overline{x}_1-\overline{x}_2)=\sqrt{(s_1^2)/(n_1)+(s_2^2)/(n_2)}`

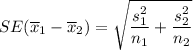
Given :
`s_1=5,\ s_2=3\ , n_1=13,\ n_2=10`

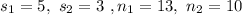
Then , the standard deviation of the difference between the two means will be :-

`SE (\overline{x}_1-\overline{x}_2)=\sqrt{((5)^2)/(13)+((3)^2)/(10)}\\\\=\sqrt{(25)/(13)+(9)/(10)}\\\\=√(1.9231+0.9)\\\\=√(2.8231)=1.680`

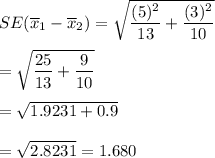
Hence, the correct answer is B. 1.679