Question

Complete the coordinate proof of the theorem. Given: ABCD is a parallelogram. Prove: The diagonals of ​ ABCD ​ bisect each other. The coordinates of parallelogram ABCD are A(0, 0) , B(a, 0) , C(a+c, b) , and D( , ). The coordinates of the midpoint of AC¯¯¯¯¯ are ( ​ a+c2 ​, ). The coordinates of the midpoint of BD¯¯¯¯¯ are ( ,​ b2 ​). The midpoints of the diagonals have the same coordinates. Therefore, the diagonals of ​ ABCD ​ bisect each other.

Answer 1

Complete proof for diagonals of ABCD bisect each other.

Explanation:

We have to complete the coordinates to complete the proof.

Mid point Formula:

Let
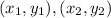`(x_1, y_1), (x_2, y_2)` be the coordinates of the endpoints whose midpoint we have to find.

Let (x,y) the the midpoint of given line segment.

Then, the coordinate of mid point are calculated with the help of following formula:

`(x,y) = \Bigg(\displaystyle(x_1+x_2)/(2), \displaystyle(y_1+y_2)/(2)\Bigg)`

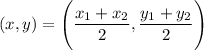
Given: ABCD is a parallelogram.

Proof:

The diagonals of ​ ABCD ​ bisect each other.

The coordinates of parallelogram ABCD are A(0, 0) , B(a, 0) , C(a+c, b) , and D(c ,b).

The coordinates of the midpoint of AC will be calculated with the help of mid point formula.

`A(0, 0) , C(a+c, b)\\\text{Coordinates of midpoint AC }= \Bigg(\displaystyle(0+a+c)/(2), \displaystyle(0+b)/(2)\Bigg) = \Bigg((a+c)/(2),(b)/(2)\Bigg)`

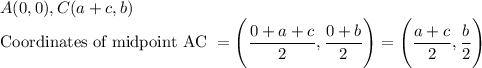
The coordinates of the midpoint of BD will be calculated with the help of mid point formula.

`B(a, 0), D( c, b).\\\text{Coordinates of midpoint of BD }= \Bigg(\displaystyle(a+c)/(2), \displaystyle(0+b)/(2)\Bigg) = \Bigg((a+c)/(2),(b)/(2)\Bigg)`

The midpoints of the diagonals have the same coordinates.

Therefore, the diagonals of ​ ABCD ​ bisect each other.