Question

A boater travels 27 miles per hour on the water on a still day. During one particularly windy​ day, he finds that he travels 42 miles with the wind behind him in the same amount of time that he travels 21 miles into the wind. Find the rate of the wind.

Answer 1

The rate of wind is 9 miles per hour.

Explanation:

We are given the following information:

A boater travels 27 miles per hour on the water on a still day.

`\text{Speed} = \displaystyle\frac{\text{Distance}}{\text{Time}}\\\\\text{Time} = \displaystyle\frac{\text{Distance}}{\text{Speed}}`

The w be the rate of wind.

27 + w = speed with the wind

27 - w = speed against the wind

Time taken by him to travel with the wind =

`\displaystyle(42)/(27+w)`

Time taken by him to travel against the wind =

`\displaystyle(21)/(27-w)`

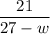
Since, the time is equal,

`\displaystyle(42)/(27+w) = \displaystyle(21)/(27-w)\\\\42(27-w) = 21(27+w)\\1134 - 42w = 567 + 21w\\63w = 567\\\\w = (567)/(63) = 9`

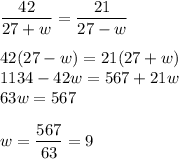
Thus, the rate of wind is 9 miles per hour.