Answer:
The required steps are shown below:
Explanation:
Consider the provided information.
Substitution property: If x = y, then one can replace x with y.
Alternate interior angles: If two lines are crossed by transversal , a pair of angles on the inner sides of each of these two lines on the opposite sides of the transversal line is called alternate interior angle.
Alternating interior angles theorem: If two parallel lines are intersected by third lines, the angles in the inner sides of the parallel lines on the opposite sides of the transversal are equal.
Now use above information to prove

Statement Reason:
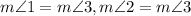 Given
Given
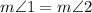 Substitution property of equality
Substitution property of equality
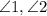 Definition of alternate interior angles
Definition of alternate interior angles
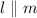 alternate interior angles are equal
alternate interior angles are equal