Answer:
1.36 times
Step-by-step explanation:
gSE=G ×
 .........................................(1)
.........................................(1)
gSV= G ×
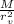 .........................................(2)
.........................................(2)
where
gSE= gravitational field of the sun on the earth
gSV= gravitational field of the sun on venus
M= mass of the sun
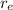 = distance of the earth from the sun
= distance of the earth from the sun
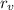 = distance of venus from the sun
= distance of venus from the sun
form equation 1,
GM = gSE ×
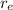 ².....................................(3)
².....................................(3)
from equation 2,
GM = gSV ×
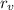 ²......................................(4)
²......................................(4)
equating equation 3 and 4
gSE ×
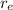 ² = gSV ×
² = gSV ×
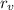 ²
²
gSV = gSE × (
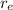 ² ÷
² ÷
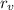 ²)
²)
= gSE ×
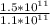
gSv= gSE × 1.36
∴ the gravitional field of the sun on venus (gSV) is 1.36 times the gravitational field on the earth (gSE)