Question

Suppose a research paper states that the distribution of the daily sea-ice advance/retreat from each sensor is similar and is approximately double exponential. The proposed double exponential distribution has density function f(x) = 0.5λe−λ|x| for −[infinity] < x < [infinity]. The standard deviation is given as 38.3 km. (Round your answers to four decimal places.) (a) What is the value of the parameter λ?

Answer 1

The value of the parameter is λ is 0.03692

Explanation:

Consider the provided function.

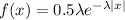`f(x) = 0.5\lambda e^(-\lambda |x|)` for −∞ < x < ∞.

It is given that standard deviation is given as 38.3 km.

Now we need to calculate the value of parameter λ.

The general formula for the probability density function of the double exponential distribution is:
`f(x)=\frac{e^(x-\mu)/(\beta)}{2\beta}`

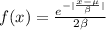
Where μ is the location parameter and β is the scale parameter.

Compare the provided equation with the above formula we get.

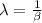`\lambda=(1)/(\beta)` and μ = 0.

Standard deviation = √2β

`S.D=√(2) \beta\\\beta=(38.3)/(√(2))\\\beta=27.08219`

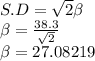
Now substitute the value of β in
`\lambda=(1)/(\beta)`.

`\lambda=(1)/(27.08219)=0.03692`

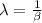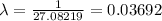
Hence, the value of the parameter is λ is 0.03692