Question

You and your friend are comparing two loan options for a $165,000 house. Loan 1 is a 15-year loan with an annual interest rate of 3%. Loan 2 is a 30-year loan with an annual interest rate of 4%. Your friend claims the total amount repaid over the loan will be less for Loan 2. Is your friend correct? Justify your answer.

Answer 1

No, he is wrong.

Explanation:

Since, the total payment of a loan after t years,

`A=P(1+r)^t`

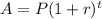
Where,

P = present value of the loan,

r = rate per period ,

n = number of periods,

Given,

P = $165,000,

In loan 1 :

r = 3% = 0.03, t = 15 years,

So, the total payment of the loan is,

`A_1 = 165000(1+0.03)^(15)=165000(1.03)^(15)\approx \$ 257,064.62`

In loan 2 :

r = 4% = 0.04, t = 30 years,

So, the total payment of the loan is,

`A_2 = 165000(1+0.04)^(30)=165000(1.04)^(30)\approx \$ 535,160.59`

Since,
`A_1 < A_2`

Hence, total amount repaid over the loan will be less for Loan 1.

That is, the friend is wrong.