Question

6. A 15 kg box is given an initial push so that it slides across the floor and comes to a stop.

If the coefficient of friction is 0.30,
fn=(15)(-9.8) = 147.15
a) find the friction force.
(30 (142.15
b) find the acceleration of the box.
c) how far will the box go if its initial speed is 3.0 m/s?

Answer 1

(a) Frictional force = 44.145 N

(b) Acceleration = -2.943 m/s²

(c) Distance covered = 1.529 m

Step-by-step explanation:

Given:

Mass of the box is,
`m=15\ kg`

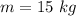
Coefficient of friction is,
`\mu =0.30`

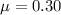
Acceleration due to gravity is,
`g=9.81\ m/s^2`

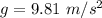
Normal force acting on the box is,
`N=mg=(15)(9.81) = 147.15\ N`

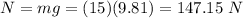
(a)

Frictional force is given as:

`f=\mu N=0.30* 147.15=44.145\ N`

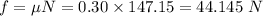
Therefore, the frictional force is 44.145 N.

(b)

The acceleration of the box is given using Newton's second law as:

`a=-(f)/(m)=-(44.145)/(15)=-2.943\ m/s^2`

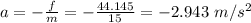
Therefore, the acceleration of the box is -2.943 m/s².

(c)

Initial velocity is,
`u=3.0\ m/s`

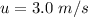
Final velocity is,
`v=0\ m/s`

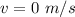
Acceleration of the box is,
`a=-2.943\ m/s^2`

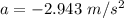
The displacement of the box can be determined using equation of motion as:

`v^2=u^2+2ad\\0=3^2+2* (-2.943)d\\0=9-5.886d\\5.886d=9\\d=(9)/(5.886)=1.529\ m`

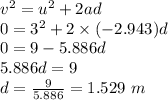
Therefore, the displacement of the box is 1.529 m.