Question

My Notes The displacement from equilibrium of an oscillating weight suspended by a spring is given by y(t) = 1 4 cos(5t) where y is the displacement (in feet) and t is the time (in seconds). Find the displacement when t = 0, t = 1 4 , and t = 1 2 . (Round your answers to four decimal places.)

a) t = 0 y(0) = ft
(b) t = 1 4 y 1 4 = ft
(c) t = 1 2 y 1 2 = ft

Answer 1

y(0) = 0.25 feet

`y((1)/(4)) = 0.0789 \text{ feet}`

`y((1)/(2)) =-0.2003 \text{ feet}`

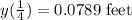
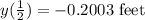
Explanation:

We are given the following information in the question:

The displacement from equilibrium of an oscillating weight suspended by a spring =

`y(t) = \displaystyle(1)/(4) \cos(5t)`

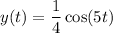
where y is the displacement in feet and t is the time in seconds.

Here, cos is in radians.

1) t = 0

`y(0) = \displaystyle(1)/(4) \cos(5(0)) = (1)/(4) \cos(0) = (1)/(4)(1) = (1)/(4)`

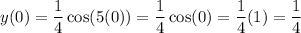
y(0) = 0.25 feet

2) t =
`(1)/(4)`

`y(\displaystyle(1)/(4)) = \displaystyle(1)/(4) \cos(5((1)/(4))) = (1)/(4) \cos(1.25) = (1)/(4)(0.31532236) =0.07883059`

`y((1)/(4)) = 0.0789 \text{ feet}`

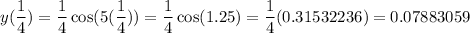
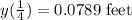
3) t =
`(1)/(2)`

`y(\displaystyle(1)/(2)) = \displaystyle(1)/(4) \cos(5((1)/(2))) = (1)/(4) \cos(2.5) = (1)/(4)(-0.80114362) = -0.200285905`

`y((1)/(2)) =-0.2003 \text{ feet}`

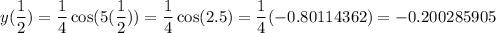
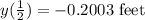
The negative sign indicates the opposite direction of displacement.