Answer:
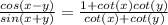
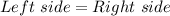 , hence the identity is verified.
, hence the identity is verified.
Explanation:
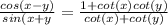
Working on right hand side.
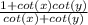
Substituting
![[cot(x)=(cos(x))/(sin(x))]](https://img.qammunity.org/2020/formulas/mathematics/college/ee5agbh8kvnhrgpfkw6x4wswvmludp2n7k.png) and
and
![[cot(y)=(cos(y))/(sin(y))]](https://img.qammunity.org/2020/formulas/mathematics/college/ccmll0rmgi1m9wipevivkzsy5igwd877co.png)
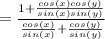
Taking LCD and adding fractions.

Cancelling out the common denominators.
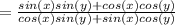
Applying sum and difference formulas
![[cos(x-y)=cos(x)cos(y)-sin(x)sin(y)][sin(x+y)=sin(x)cos(y)+sin(y)cos(x)]](https://img.qammunity.org/2020/formulas/mathematics/college/3vduedf9ue349su10enjuao7117ypc5921.png)
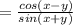
Left side

∵
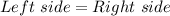 , hence the identity is verified.
, hence the identity is verified.