Answer:
The marble lands at a distance of 1.36 m from the base of the table.
Step-by-step explanation:
The motion of the marble falling off the table is a projectile with initial velocity in the horizontal direction only.
The motion can be solved in two directions, the horizontal and vertical direction.
Along the vertical direction, the initial velocity is 0 m/s as it has only horizontal component initially. Also acceleration in the vertical direction is acceleration due to gravity.
Let us use equation of motion in vertical direction.

Where,

Now, plug in 0 for
 ,
,
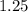 for
for
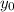 , 0 for
, 0 for
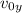 , -9.8 for
, -9.8 for
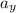 . This gives,
. This gives,
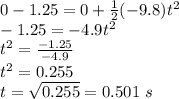
Therefore, time to reach bottom is 0.501 s.
Now, consider the horizontal motion. There is no acceleration in the horizontal direction. So, distance is given as the product of horizontal velocity and time taken.
Horizontal distance covered by the marble is given as:
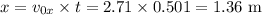
Therefore, the marble lands at a distance of 1.36 m from the base of the table.