Question

A bicycle tire is spinning clockwise at 3.40 rad/s. During a time period Δt = 2.50 s, the tire is stopped and spun in the opposite (counterclockwise) direction, also at 3.40 rad/s. Calculate the change in the tire's angular velocity Δω and the tire's average angular acceleration αav. (Indicate the direction with the signs of your answers.)

Answer 1

The change in the tire's angular velocity is
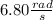`6.80(rad)/(s)`. The tire's average angular acceleration is
`2.72(rad)/(s^2)`

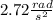
Step-by-step explanation:

Let's assume that the counterclockwise direction is the positive direction, then, as we were given the initial and final angular velocity (ω) and there is a direction change between them, we can calculate the change in angular velocity as

`\Delta\omega=\omega_(f)-\omega_(i)=3.40(rad)/(s)-(-3.40(rad)/(s))=6.80(rad)/(s)`

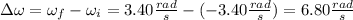
On the other hand, to calculate the average angular acceleration we have that

`\alpha_(av)=(\Delta\omega)/(\Delta t)`

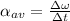
we just calculated Δω, and Δt is given in the problem, therefore

`\alpha_(av)=(\Delta\omega)/(\Delta t)=(6.80rad)/(2.50s^2)=2.72(rad)/(s^2)`

is the average angular acceleration of the tire.