Question

A coffee filter in the shape of an inverted cone (8 inches in diameter and 4 inches tall) is dripping coffee. There is a cylindrical coffee pot (10 inches in diameter and 6 inches tall) below the cone. How fast is the height of the coffee in the pot increasing when the level of coffee in the filter is 2 inches and decreasing at a rate of .2 inches per second?

Answer 1

0.032 inches per second

Step-by-step explanation:

The volume of the conic filter is given by:

`Vf = \pi *R^2*h/3`

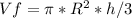
The relation between the height and radius is:

R = (8inches/2)/4inches*h

R = h Replacing this:

`Vf = \pi *h^3/3`

The derivative of the volume is:

`Vf'=3*\pi*h^2*h'/3`

`Vf'=3*\pi*(2)^2*(-0.2)/3=-0.8*\pi`

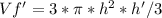
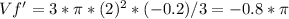
The decreasing rate change on the filter's volume is the same increasing change rate on the coffee pot's volume. Since the volume of the pot is:

`Vp=\pi*R^2*h`

The derivative is:

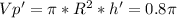`Vp'=\pi*R^2*h'=0.8\pi` where h' is the change rate in its height:

h' = 0.032 inches/s