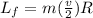Answer:
initial angular momentum is given as

final angular momentum is given as
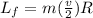
Step-by-step explanation:
Angular momentum of the ball about the axis of the thin walled sphere is given as
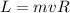
here we know that
before it grazes the surface the speed is "v" while after grazing the surface its speed is "v/2"
So we have
initial angular momentum is given as

final angular momentum is given as