Question

A total of 46 percent of voters in a certain city classify themselves as Independents, whereas 30 percent classify themselves as Liberals and 24 percent Conservatives. In a recent local election, 35 percent of the Independents, 62 percent of the Liberals, and 58 percent of the Conservatives voted. A voter is chosen at random. Given that this person in the local election, what is the probability that he or she is:

(a) an Independent
(b) a Liberal
(c) a conservative
(d) What fraction of voters participated in the local election?

Answer 1

a) Given that this person voted in the local election, there is a 33.11% proabability that he or she is an Independent.

b) Given that this person voted in the local election, there is a 38.26% proabability that he or she is a Liberal.

c) Given that this person voted in the local election, there is a 28.63% proabability that he or she is a conservative.

d) 48.62% of voters participated in the local election.

Explanation:

We have these following percentages:

46% of the voters in the city are Independents.

30% of the voters in the City are Liberals

24% of the voters in the City are Conservatives.

In a recent election

35% of the Independents voted

62% of the Liberals voted

58% of the Conservatives voted.

Given that this person voted in the local election, what is the probability that he or she is:

The first step to solve this problem is finding the fraction of voters that participated in the local election, that is, question d.

(d) What fraction of voters participated in the local election?

This is the sum of 35% of 46%, 62% of 30%, 58% of 24%. So:

`P = 0.35*0.46 + 0.62*0.30 + 0.58*0.24 = 0.4862`

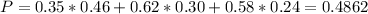
48.62% of voters participated in the local election.

(a) an Independent

46% of the people are independent, and 35% of them voted.

So the probability that the person is an independent, given that she voted is:

`P = (0.46*0.35)/(0.4862) = 0.3311`

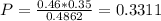
Given that this person voted in the local election, there is a 33.11% proabability that he or she is an Independent.

(b) a Liberal

30% of the people are Liberal, and 62% of them voted.

So the probability that the person is a Liberal, given that she voted is:

`P = (0.30*0.62)/(0.4862) = 0.3826`

Given that this person voted in the local election, there is a 38.26% proabability that he or she is a Liberal.

(c) a conservative

24% of the people are Liberal, and 58% of them voted.

So the probability that the person is a conservative, given that she voted is:

`P = (0.24*0.58)/(0.4862) = 0.2863`

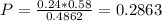
Given that this person voted in the local election, there is a 28.63% proabability that he or she is a conservative.