Question

N a certain store, there is a .03 probability that the scanned price in the bar code scanner will not match the advertised price. The cashier scans 780 items.

(a) What is the expected number of mismatches? (Round your answer to the nearest whole number.)
(b) What is the standard deviation? (Use your rounded number for the expected number of mismatches for the calculation of standard deviation. Round your final answer to 4 decimal places.)

Answer 1

Explanation:

Given that in a certain store, there is a .03 probability that the scanned price in the bar code scanner will not match the advertised price.

Here X the number of items that will not match in the sample of 780 items is binomial because

i) there are two outcomes only

ii) Also each trial is independent of the other.

a) the expected number of mismatches

`=E(X) = 780(0.03)\\= 23.40\\=23`

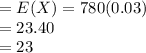
b) Var(x) =
`npq = 780(0.03)(0.97)\\= 22.698`

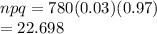
Std dev (X) = 4.7642