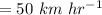Question

With a given head wind, a plane can fly 3000 km in 6 hours. Flying in the opposite direction with the same wind blowing, the plane can fly the same distance in 5 hours. Find the planes air speed and the speed of the wind.

Answer 1

Air speed of plane
`=550\ km\ hr^(-1)`

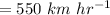
Speed of wind
`=50\ km\ hr^(-1)`

Explanation:

Given:

Distance = 3000 km

Time, the plane takes to cover the distance opposite wind direction= 6 hours

Time, the plane takes to cover the distance in wind direction= 5 hours

∴ Speed in opposite wind direction
`=(Distance)/(Time)=(3000)/(6)=500\ km\ hr^(-1)`

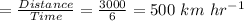
∴ Speed in windward direction
`=(Distance)/(Time)=(3000)/(5)=600\ km\ hr^(-1)`

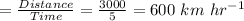
Let air speed of plane be
`=x\ km\ hr^(-1)`

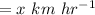
Let speed of wind be
`=y\ km\ hr^(-1)`

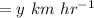
Speed in opposite wind direction
`=(x-y)\ km\ hr^(-1)`

Speed in wind direction is
`=(x+y)\ km\ hr^(-1)`

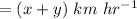
Substituting the known values, we can get two equations.

1)
`x-y=500`

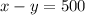
2)
`x+y=600`

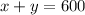
Adding the above equations we get:

`2x=1100`

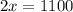
dividing both sides by 2.

`(2x)/(2)=(1100)/(2)`

∴
`x=550`

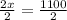
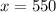
Substituting the value of
`x` in equation (2) to find
`y`

we get
`550+y=600`

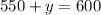
Subtracting both sides by 550.

`550+y-550=600-550`

∴
`y=50`

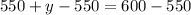
Air speed of plane
`=550\ km\ hr^(-1)`

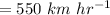
Speed of wind
`=50\ km\ hr^(-1)`