Question

*****PLEASE HELP (30 POINTS)*****

2. Find the area of the given equilateral triangle. Round your answer to the nearest tenth.

(No, there is nothing missing from the given figure. Yes, there is enough info given in the figure to answer this question.)
A) 73.5 yd2
B) 14.4 yd2
C) 21.2 yd2
D) 42.4 yd2

3. Name the central angle of the given arc.
A) angle IQJ
B) angle IQL
C) angle JQK
D) angle JQL

4.Find the measure of the angle indicated by a "?."
A) 39 degrees
B) 55 degrees
C) 34 degrees
D) 59 degrees

Answer 1

2. C) 21.2 yd 3. B) angle IQL 4. B) 55 degree

Explanation:

2. The area of an equilateral triangle is given by,

A =
`\frac {√(3) * a^(2)}{4}`------(1) where a = length of each side.

Here, a = 7 yd

so , putting a = 7 yd in (1) , we get,

A =
`\frac {√(3) * 49}{4}` sq. yd.

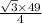`\simeq 21.2` sq. yd.

3. B) angle IQL

4. Let, the centre of the circle be at O,

then, ∠DOB = 105° and ∠BOC = 145° (given)

so, ∠OBD =
`(180^(\circ) - \angle DOB)/(2)`

=
`(180^(\circ) - 105^(\circ))/(2)`

= 37.5° [since the sum of three angles of a triangle is 180° and OB and OD are two radii of the same circle]

and, similarly, ∠OBC =
`(180^(\circ) - \angle COB)/(2)`

=
`(180^(\circ) - 145^(\circ))/(2)`

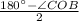
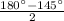
= 17.5° [since the sum of three angles of a triangle is 180° and OB and OC are two radii of the same circle]

so, ∠CBD = ∠OBD + ∠OBC

= 37.5° + 17.5°

= 55°