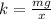Question

A light spring with spring constant 1300 N/m hangs from an elevated support. From its lower end hangs a second light spring, which has spring constant 1700 N/m. An object of mass 1.50 kg is hung at rest from the lower end of the second spring.(a) Find the total extension distance of the pair of springs.= m(b) Find the effective spring constant of the pair of springs as a system. We describe these springs as in series.= N/m

Answer 1

Part a)

`x = 0.02 m`

Part b)

`k = 737 N/m`

Step-by-step explanation:

Let say the extension of spring 1 is x1 and extension of spring 2 is x2

then we will have

`k_1x_1 = k_2x_2 = mg`

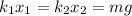
so we will have

`x_1 = (mg)/(k_1)`

`x_1 = (1.50 * 9.81)/(1300)`

`x_1 = 0.0113 m`

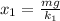
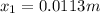
for other spring we will have

`x_2 = (mg)/(k_2)`

`x_2 = (1.50 * 9.81)/(1700)`

`x_2 = 0.00866 m`

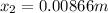
so total extension of both the springs is given as

`x = x_1 + x_2`

`x = 0.0113 + 0.00866`

`x = 0.02 m`

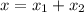
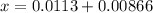
Part b)

Let say the effective spring constant is k

so we will have

`kx = mg`

`k = (mg)/(x)`

`k = (1.5 * 9.81)/(0.02)`

`k = 737 N/m`