Question

If a(x) = 2x - 4 and b(x) = X + 2, which of the following expressions produces a quadratic function?

O (ab)(x)
O (a - b)(x)
O (a + b)(x)

Answer 1

`(ab)(x)` Produces quadratic function

Solution:

Given that

a (x) = 2x – 4 and b(x) = x + 2

Need to check which of the expression from given three expression produce a quadratic function. Let us solve each option and check the result.

`(a b)(x)=a(x) * b(x)=(2 x-4) *(x+2)`

`\begin{array}{l}{=x(2 x-4)+2(2 x-4)} \\\\ {=2 x^(2)-4 x+4 x-8} \\\\ {=2 x^(2)-8}\end{array}`

`\Rightarrow \quad(a b)(x)=2 x^(2)-8`

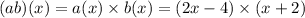
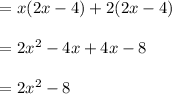
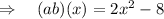
So (ab)(x) produces a quadratic function
`2x^2-8.`

`\text { 2) }(a-b)(x)=a(x)-b(x)=(2 x-4)-(x+2)`

`\begin{array}{l}{=(2 x-4)-(x+2)} \\\\ {=2 x-4-x-2} \\\\ {=x-6}\end{array}`

`\Rightarrow(a-b)(x)=x-6`

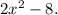
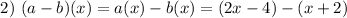
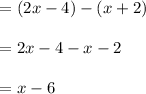
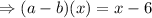
So (a - b)(x) produces a linear function x – 6.

`\begin{array}{l}{\text { 3) }(a+b)(x)=a(x)+b(x)=(2 x-4)+(x+2)} \\\\ {=(2 x-4)+(x+2)} \\\\ {=2 x-4+x+2} \\\\ {=x-2}\end{array}`

`\Rightarrow(a+b)(x)=x-2`

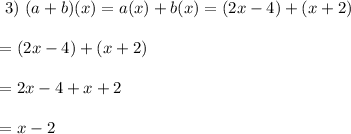
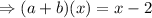
So (a + b)(x) produces a linear function x – 2.

Hence we can conclude that (ab)(x) produces quadratic function.