Question

A block of mass 3m is released from rest at a height R above a horizontal surface. Theacceleration due to gravity is g. The block slides along the inside of a frictionless circular hoop of radius R. What is the magnitude of the normal force exerted on the block by the hoop when the block has reached the bottom?

Answer 1

N = 3 mg

Step-by-step explanation:

For this case we will use Newton's second law where acceleration is centripetal.

F = m a

a = v² / r

Let's write the expression for the lowest part of the hoop

N- W = m a

N = mg + m V2 / r

To find the speed let's use energy conservation

highest point

Em₀ = U = m g y

lowest point

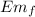`Em_(f)` = K = ½ m v²

Em₀ =
`Em_(f)`

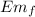
mg y = ½ m v²

v = √ 2gy

We substitute in the equation of the normal

N = m (g 2g y/r )

Let's analyze the initial height it gives is that the body leaves a height R

N = m (g + 2 g R / R)

N = 3 mg