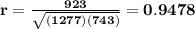Question

Consider the given data. x 0 2 4 6 9 11 12 15 17 19 y 5 6 7 6 9 8 8 10 12 12 Use the least-squares regression to fit a straight line to the given data. Along with the slope and intercept, compute the standard error of the estimate and the correlation coefficient. Repeat the problem, but regress x versus y—that is, switch the variables. Interpret your results. (Round the final answers to four decimal places.) Least-squares regression: y versus x B

Answer 1

See below

Explanation:

By using the table 1 attached (See Table 1 attached)

We can perform all the calculations to express both, y as a function of x or x as a function of y.

Let's make first the line relating y as a function of x.

y as a function of x

(y=response variable, x=explanatory variable)

`\bf y=m_(yx)x+b_(yx)`

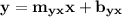
where

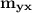`\bf m_(yx)` is the slope of the line

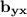`\bf b_(yx)` is the y-intercept

In this case we use these formulas:

`\bf m_(yx)=((\sum y)(\sum x)^2-(\sum x)(\sum xy))/(n\sum x^2-(\sum x)^2)`

`\bf b_(yx)=(n\sum xy-(\sum x)(\sum y))/(n(\sum x^2)-(\sum x)^2)`

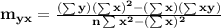
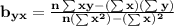
n = 10 is the number of observations taken (pairs x,y)

Note: Be careful not to confuse

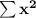`\bf \sum x^2` with
`\bf (\sum x)^2`

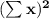
Performing our calculations we get:

`\bf m_(yx)=((83)(95)^2-(95)(923))/(10*1277-(95)^2)=176.6061`

`\bf b_(yx)=(10*923-(95)(83))/(10(1277)-(95)^2)=0.3591`

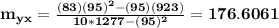
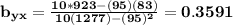
So the equation of the line that relates y as a function of x is

y = 176.6061x + 0.3591

In order to compute the standard error
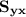`\bf S_(yx)`, we must use Table 2 (See Table 2 attached) and use the definition

`\bf s_(yx)=\sqrt{((y-y_(est))^2)/(n)}`

and we have that standard error when y is a function of x is

`\bf s_(yx)=\sqrt{(39515985)/(10)}=1987.8628`

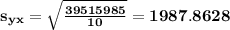
Now, to find the line that relates x as a function of y, we simply switch the roles of x and y in the formulas.

So now we have:

x as a function of y

(x=response variable, y=explanatory variable)

`\bf x=m_(xy)y+b_(xy)`

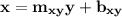
where

`\bf m_(xy)` is the slope of the line

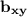`\bf b_(xy)` is the x-intercept

In this case we use these formulas:

`\bf m_(xy)=((\sum x)(\sum y)^2-(\sum y)(\sum xy))/(n\sum y^2-(\sum y)^2)`

`\bf b_(xy)=(n\sum xy-(\sum x)(\sum y))/(n(\sum y^2)-(\sum y)^2)`

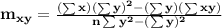
n = 10 is the number of observations taken (pairs x,y)

Note: Be careful not to confuse

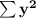`\bf \sum y^2` with
`\bf (\sum y)^2`

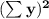
Remark: If you wanted to draw this line in the classical style (the independent variable on the horizontal axis), you would have to swap the axis X and Y)

Computing our values, we get

`\bf m_(xy)=((95)(83)^2-(83)(923))/(10*743-(83)^2)=1068.1072`

`\bf b_(xy)=(10*923-(95)(83))/(10(743)-(83)^2)=2.4861`

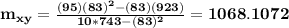
and the line that relates x as a function of y is

x = 1068.1072y + 2.4861

To find the standard error
`\bf S_(xy)` we use Table 3 (See Table 3 attached) and the formula

`\bf s_(xy)=\sqrt{((x-x_(est))^2)/(n)}`

and we have that standard error when y is a function of x is

`\bf s_(xy)=\sqrt{(846507757)/(10)}=9200.5856`

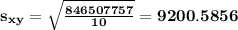
In both cases the correlation coefficient r is the same and it can be computed with the formula:

`\bf r=(\sum xy)/(√((\sum x^2)(\sum y^2)))`

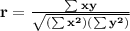
Remark: This formula for r is only true if we assume the correlation is linear. The formula does not hold for other kind of correlations like parabolic, exponential,..., etc.

Computing the correlation coefficient :

`\bf r=(923)/(√((1277)(743)))=0.9478`