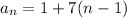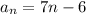Question

Write the recursive formula for the following sequence
1, 8, 15, 22, 29, 36, …

Answer 1

`a_n=7n-6`

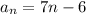
Explanation:

we have

`1, 8, 15, 22, 29, 36,...`

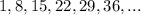
we know that

An arithmetic sequence is a sequence of numbers such that the difference of any two successive members of the sequence is a constant. This constant is called the common difference

Let

`a_1=1\\a_2=8\\a_3=15\\a_4=22\\a_5=29\\a_6=36`

`a_2-a_1=8-1=7\\a_3-a_2=15-8=7\\a_4-a_3=22-15=7\\a_5-a_4=29-22=7\\a_6-a_5=36-29=7`

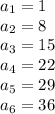
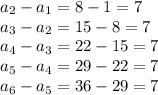
The common difference is equal to 7

therefore

The recursive formula is equal to

`a_n=a_1+d(n-1)`

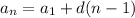
where

n is the number of terms

d is the common difference

we have

`d=7`

`a_1=1`

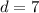
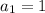
substitute

`a_n=1+7(n-1)`

`a_n=1+7n-7`

`a_n=7n-6`