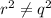Question

Given that n^2+2pn+p^2+q^2=r^2 has real roots show that r^2=q^2

​

Answer 1

It doesn't seem true, and here's a counterexample: observe that the first three terms form a perfect square. You can rewrite the equation as

`(n+p)^2+q^2=r^2`

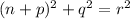
This is basically the Pythagorean theorem applied to a triangle with sides n+p, q and r. For example, pick:

`n=1, p=2, q=4, r^5`

The expression becomes

`1^2+2\cdot 2\cdot 1+2^2+4^2=5^2 \iff 1+4+4+16=25 \iff 25=25`

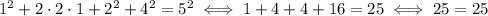
Which is true, even if

`r^2\\eq q^2`