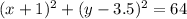Answer:
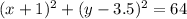
Explanation:
We are given that endpoints of a diameter at the points (7,2) and (-9,5).
Center of the circle is the mid point of diameter
So, first find the mid point of diameter
Formula :
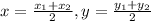
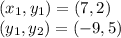
Substitute the values in formula

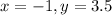
So, center of circle = (h,k )=(-1,3.5)
To find length of diameter :

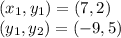
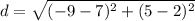

Length of radius = r =
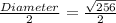
Standard form of the equation of the circle :
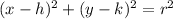
(h,k )=(-1,3.5)
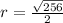
Equation of the circle :
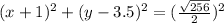
Equation of the circle :
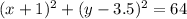
Hence the standard form of the equation of the circle with endpoints of a diameter at the points (7,2) and (-9,5) is