Question

The diffrence of two fractions is 1/3. The sum of these two fractions is 1. The quotient of rge larger fraction divided by the smaller fraction is 2. What are the two fractions?

Answer 1

The earliest fractions were reciprocals of integers: ancient symbols representing one part of two, one part of three, one part of four, and so on. The Egyptians used Egyptian fractions c. 1000 BC. About 4000 years ago, Egyptians divided with fractions using slightly different methods. They used least common multiples with unit fractions. Their methods gave the same answer as modern methods. The Egyptians also had a different notation for dyadic fractions in the Akhmim Wooden Tablet and several Rhind Mathematical Papyrus problems.

The Greeks used unit fractions and (later) continued fractions. Followers of the Greek philosopher Pythagoras (c. 530 BC) discovered that the square root of two cannot be expressed as a fraction of integers. (This is commonly though probably erroneously ascribed to Hippasus of Metapontum, who is said to have been executed for revealing this fact.) In 150 BC Jain mathematicians in India wrote the "Sthananga Sutra", which contains work on the theory of numbers, arithmetical operations, and operations with fractions.

Answer 2

The fractions are
`(2)/(3)` and
`(1)/(3)`

Solution:

Given, The difference of two fractions is
`(1)/(3)`

Let the two factions be
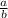`(a)/(b)` and
`(c)/(d)` ,

`\text { Where } (a)/(b)>(c)/(d)`

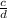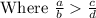
By given, difference is
`(1)/(3)` , we get

`\text { Then, } (a)/(b)-(c)/(d)=(1)/(3) \rightarrow(1)`

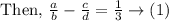
The sum of these two fractions is 1

`\text { Then, } (a)/(b)+(c)/(d)=1 \rightarrow(2)`

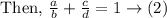
The quotient of larger fraction divided by the smaller fraction is 2.

`\text { Then, } ((a)/(b))/((c)/(a))=2 \rightarrow(3)`

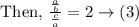
We have to find what are the two fractions

`\text { Now, }(3) \rightarrow (a)/(b)=2 * (c)/(d)`

`\text { So substitute } (a)/(b) \text { value in }(2) \text { and }(1)`

`(1) \rightarrow 2 (c)/(d)-(c)/(d)=(1)/(3) \\\\\rightarrow (c)/(d)=(1)/(3)`

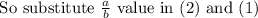
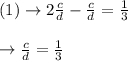
So, smaller fraction is
`(1)/(3)`

`\text { Then from }(3) \rightarrow (a)/(b)=2 * (1)/(3) \rightarrow (a)/(b)=(2)/(3)`

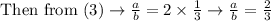
Hence, the fractions are
`(2)/(3)` and
`(1)/(3)`