Answer:
The equation
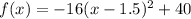 is used to find the maximum height.
is used to find the maximum height.
The maximum height of the object is 40 feet at x=1.5.
Explanation:
The vertex from of a parabola is
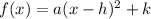 ..... (1)
..... (1)
where, a is constant, (h,k) is vertex.
The object's position at time x is given by

where, v is initial velocity and s is initial height.
It is given that the initial height of the object is 4 feet and initial velocity is 48 feet per second.
Substitute v=48 and s=4 in the above function.
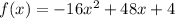
Rewrite the above equation in vertex form.
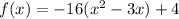
If an expression is
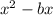 , then we need to add
, then we need to add
 in it to make it perfect square.
in it to make it perfect square.
In the parenthesis b=3,

Add and subtract (1.5)^2 in the parenthesis.
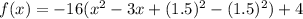
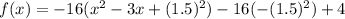

![[\because (a-b)^2=a^2-2ab+b^2]](https://img.qammunity.org/2020/formulas/mathematics/high-school/14xchlcvyv1c3qsy5ueoz3rt7wdko6uaxq.png)
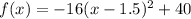 .... (2)
.... (2)
The equation
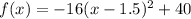 is used to find the maximum height.
is used to find the maximum height.
On comparing (1) and (2), we get
a=-16, h=1.5, k=40
Therefore, the maximum height of the object is 40 feet at x=1.5.